Applications of Quantum Computing to GW data analysis: Progress Update
Jonas Tjepkema
Project supervised by Gideon Koekoek and Claire Blackmann as internal advisor.
Special thanks to Sarah Caudill from Utrech University.
This project was done at the University of Maastricht.
Table of Content¶
- Why using quantum computing for gravitational wave research
- Collaboration efforts
- Grovers Algorithm
- Latest Developments
- Conclusion
New Generation Detectors and Data Collection¶

3G Detectors: Einstein Telescope
- Order of magnitude better amplitude sensitivity
- Detection of frequencies as low as 1 Hz
- Allows to make observations from the whole visible universe, all the wayto its dark age
Massive increase in the amount of the data to be analysed

Extract from Gravitational-Wave Data Analysis: Computing Challenges in the 3G Era, GWIC-3G Subcommittee Reports , Bird, I. et al. (2019).
$\Longrightarrow$ Modern data-analysis techniques and supercomputer are not enough for 3G detectors.
Possible solution: Quantum computing
Ideas for possible applications of QC in GW data analysis¶
- Parameter Estimation (VQE?)
- Matched Filtering (Grover's Algorithm)
- Machine Learning Models
- SVD (VQE)
- and more that we haven't thought of yet...
Collaboration Efforts¶

Expertise in Gravitational Wave Research
- Practical experience in data-analysis aspects
- Matched Filtering
- Parameter estimation

Quantum Technology
- Rydberg Atom Quantum Computer
- Practical expertise in QC
- Theoretical expertise in QC
- Working on other ideas for QC in GW
Grovers Algorithm¶
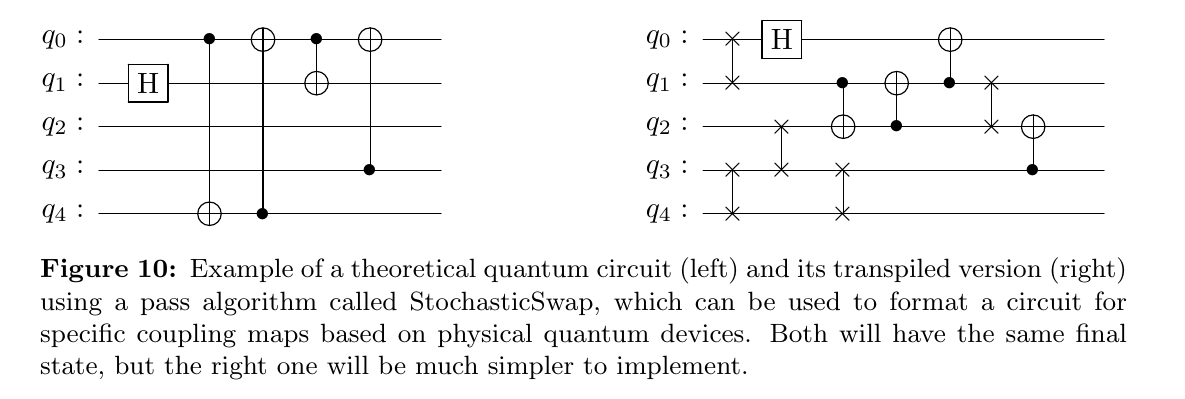
It is a quantum search algorithm. The easiest example for this is a quantum register that has been fully put to equal superposition. This is done by applying Hadamard gates to each qbit.
$$H|0\rangle H|0\rangle = |++\rangle = \left[\frac{|0\rangle+|1\rangle}{\sqrt{2}}\right]\left[\frac{|0\rangle+|1\rangle}{\sqrt{2}}\right]=\frac{1}{2}(|00\rangle+|01\rangle+|10\rangle+|11\rangle)$$This would look like a circuit,
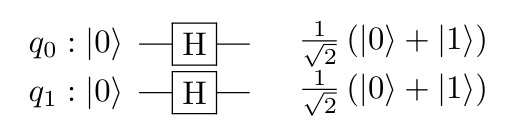
Some of the computational bases (the bases created by the combination of all the qbits). Will somehow match your search, while the others don't.
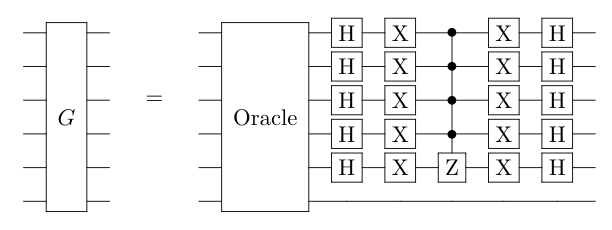
The algorithm then has two parts:
- An oracle that sifts the global phase of the solutions (no overall change if measured)
- A diffusion operator that will transfer some of the amplitude of the non-solutions to the solutions.
Grover's algorithm can be though of graphically:
- all the solution bases are combined together to form basis $|\omega\rangle$
- all the non-solutions create the orthonormal basis $|\omega_\bot\rangle$
We can then write the state as
$$ \ket{s} = \sqrt{\frac{r}{N}}\ket{w} + \sqrt{\frac{N-r}{N}}\ket{w_\bot} $$with r being the number of solutions and N being the number of elements.
The the oracle ($D_f$ operator) simply gives a negative sign/phase to the first element (process called phase kickback):
$$ D_f\ket{s} = -\sqrt{\frac{r}{N}}\ket{w} + \sqrt{\frac{N-r}{N}}\ket{w_\bot} $$and the diffusion operator reflects it on $\ket{s}$. This results in a state vector closer to $\ket{w}$, meaning the prob. of measuring a correct solution increases.
Quantum Counting¶
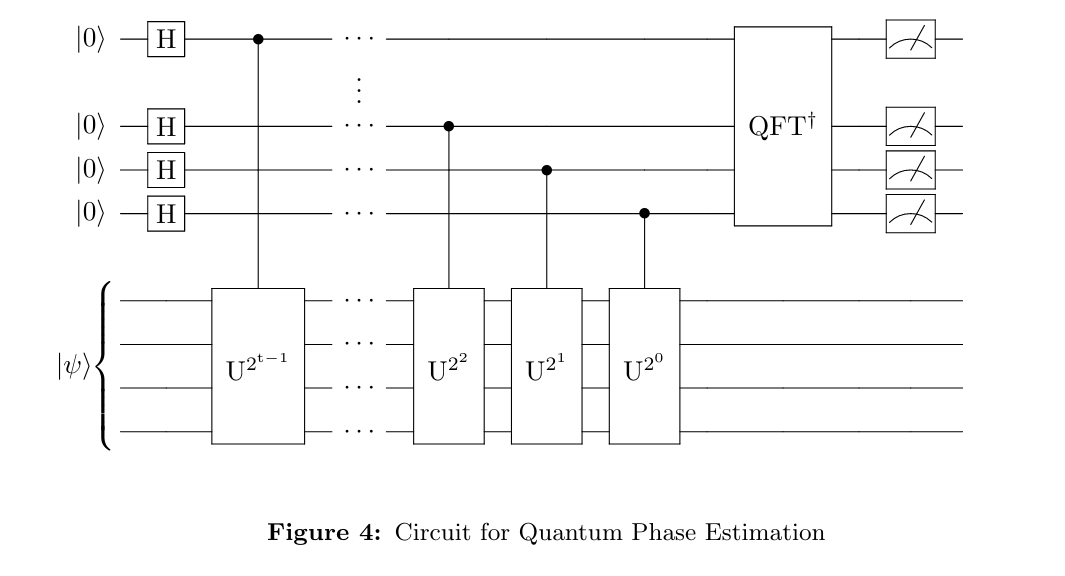
The Quantum Phase Estimation algorithm has polynomial opertational complexity (Nielsen, 2000)¶

Extract from A quantum algorithm for gravitational wave matched filtering. Uni- versity of Glasgow. Gao, S. et al. (2021); arXiv:2109.01535.
$\Longrightarrow$ Some overlap on our project
Latest developments in Maastricht¶
(Almost) Quantum Matched Filtering¶
To create a working Matched Filtering circuit, we need to be able to
- Calculate the SNRs from time-series data with quantum computing (not yet solved)
- Encode these values into QC as an array
- Encode a certain threshold SNR, $\rho_{thresh}$
- Compare the values of the SNR database
- Return the indices of all the SNRs that crossed the threshold
Database Encoding¶
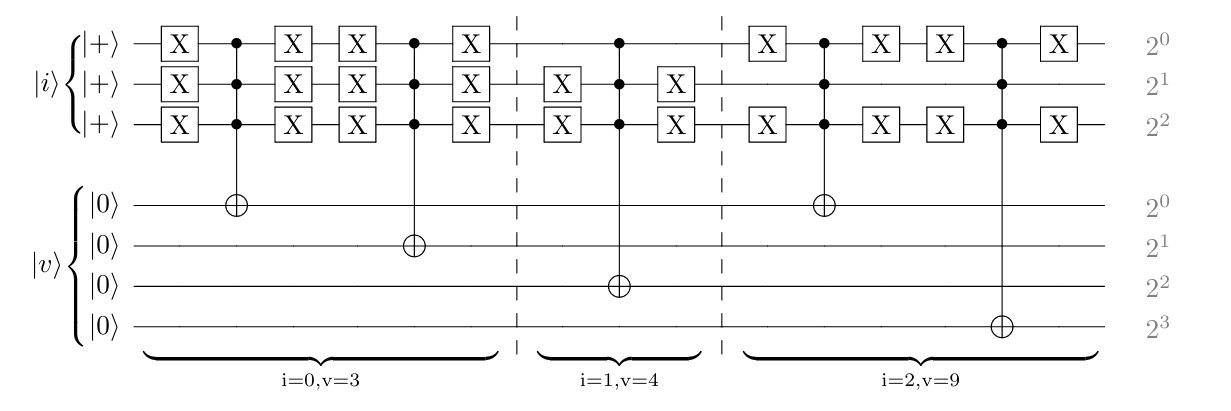
Quantum Bit String Comparator¶
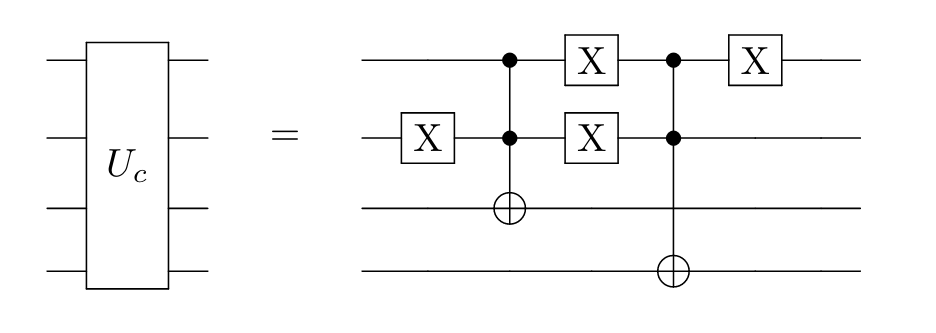
We need to be able to compare values of two bit strings. Luckily there already exists schematics for a Quantum Bit String Comparator (Oliveira et al. 2007).
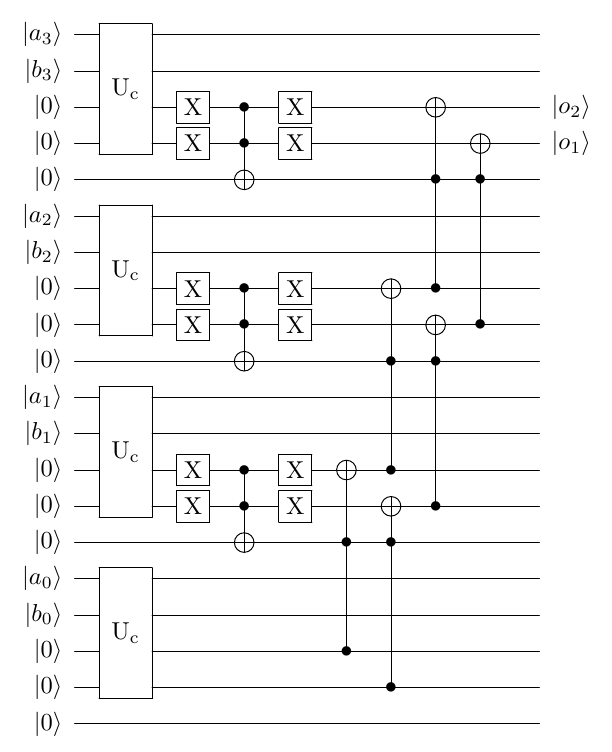
Creating the Grover Circuit¶
We need to combine:
- Data Encoding
- Bit String comparison
- Set $\rho_{thresh}$
- Disentangling
- Diffusion operator
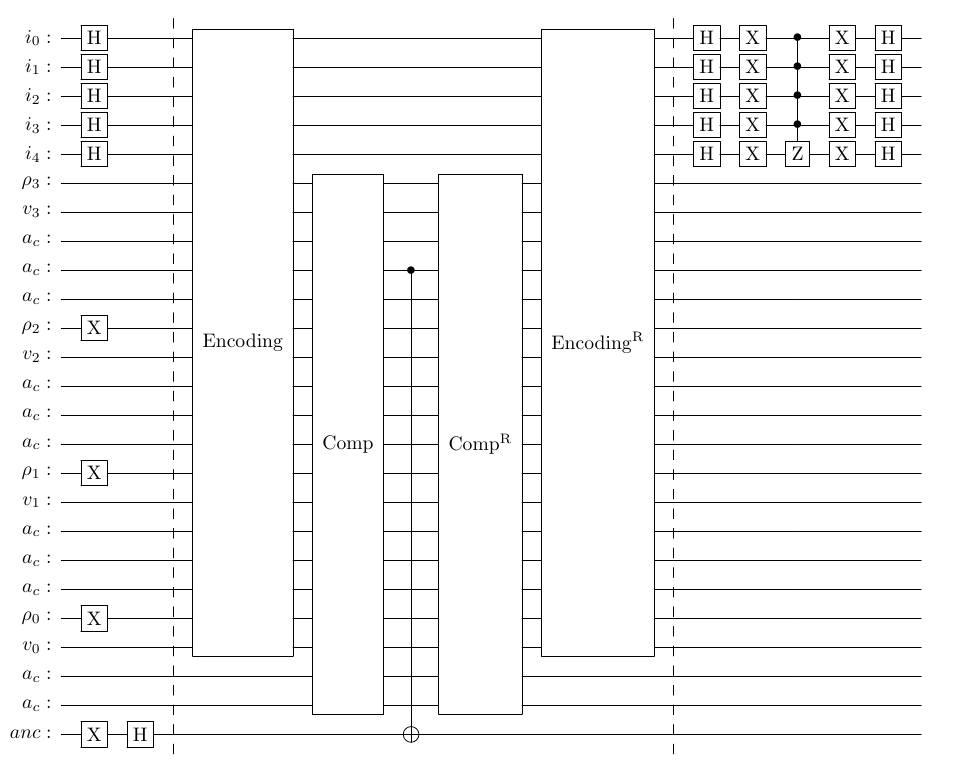
Capabilities¶
The circuit above was encoded using the values :
$$ [3,8,1,9,0,8,0,5,7,5,3,2,5,7,5,3,2,6,8,5,6,4,3,7,5,4,3,5,6,7,4,3,4,6,7\\ 8,5,3,2,2,3,4,5,4,3,2,3,4,5,6,4,3,3,3,4,5,2,2,3,4,4,4,3,2,3,4,5,6,7,6,5] $$and $$\rho_{thresh} = 7$$
This means we should be able to get an output of indices:
- 1
- 3
- 5
- 18
- 38
Total time: 48.63046964100795
Index 1 holds the value 8, which is above the chosen threshold. Index 3 holds the value 9, which is above the chosen threshold. Index 5 holds the value 8, which is above the chosen threshold. Index 18 holds the value 8, which is above the chosen threshold. Index 38 holds the value 8, which is above the chosen threshold.
Breaking down huge databases into smaller parts¶
At the moment, not enough qbits or processing power to run a full database. But by splicing:
- makes it possible to run on QC simulation (we have managed to run array length of $2^{17}$)
- lowers the hardware requirements for initial testing
Other possible benefit (currently investigated):
- Quantum counting has polynomial operational complexity
- Grover's $O(\sqrt{N})$
That means that we can possibly find an optimal splicing of parameter space to minimize some type of complexity
Testing for complexity¶
Measurment of Complexity¶
Many ways to measure complexity for quantum computing, but:
- Cannot really test time complexity on a simulator. No clear idea on speed of individual gates.
- We can however measure the evolution of the number of gates depending on the input
Impact of database and value size on Qbit number
Impact of database and value size on Qbit number
Impact of database and value size on MCX operation number
Impact of database and value size on MCX + CX operation number
Impact of database and value size on MCX + CX + X operation number